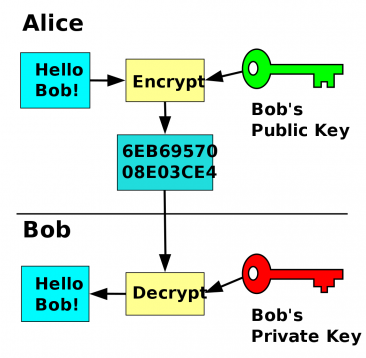
I’ve always found encryption interesting. While I’m not a mathematician I understand the basics generally. You put some data in, place it against a code, do a bunch of XOR statements and some other magic and then it comes out as crap you can’t read. To undo that, you just do it all again (in reverse) and you can suddenly read it again.
That statement mostly holds true when it comes to a symmetric encryption scheme like DES and AES, but not so much when we start talking about asymmetric encryption. For those of you who don’t remember what asymmetric encryption is, it’s an encryption scheme that uses a single key to encrypt but requires a different key to decrypt the data. You use this all the time (probably without realizing it) when you digitally sign a document or email or even encrypt your email. This is is what allows me to encrypt an email I send to someone, without having to actually trade a password or other key. The most common name for this is generally public key encryption.
As I mentioned, public key encryption makes use of two separate, but related keys. My private key is very much like you are used to. It is a secret that only I should know. If my private key gets out, then anyone can read any message of mine that they want to. With the use of digital signatures, access to your private key also allows them to sign messages as you. In short, don’t let your private key get out.
The public key on the other hand is 100% the exact opposite. With your public key, you can freely send that to anyone and everyone that you want to communicate with. And because it’s public, there really isn’t a requirement to protect it.
So how does this work, and why? I’ve tried to figure this out many times over the years because I’ve always found it really curious. I was recently redesigning an intro to computer forensics class that I teach and wanted to include some information about encryption within it. To prepare, I decided to finally search out the information that would present the idea to me in a way that I can understand (aka not being a math major).
Separate but Related
If you ever look at a public/private key pair, you will see similarities (they are both generally very long) but that’s about it. In all honesty, the two numbers are completely different (on purpose) but very close related.
Primes
The process starts with two prime numbers. If you remember from your grade school math, a prime number is any number that can only be evenly divided by itself and 1. For example, 1, 2, 3, 5, 7 are all prime numbers, however 9 is not (9 ÷ 3 = 3). Likewise, an even number can never be a prime number, because they are all divisible by 2 (at least).
We select two prime numbers at random, but these are LARGE numbers. Let me give you an example of what I mean. The number 1 Million (1,000,000) is represented in binary as 11110100001001000000 and is 2^20 bits long. Within that range (1 – 1 million) there are a total of 78,498 prime numbers in total. While prime numbers do become increasingly “rare” the larger the number (look up the Prime Number Theorem) there is still a substantial number to pick from. On top of that, like I said, we are talking about LARGE numbers. Remember, 1 million is 2^20 and most keys are at least 2^512 bits long and often times even larger then that.
Making Keys
- Pick two random large prime numbers represented as p and q. For the sake of simplicity, we are going use two very small prime numbers for our demonstration, 17 and 19. p = 17, q = 19
- n = p * q. So n = 17 * 19 = n = 323
- Now we need to determine e. e is a number that is relatively prime to (p – 1)(q-1). So what does that mean. Well first, a relatively prime number is a number that is not able to evenly divide another number. In this case we need to find a number that is relatively prime to (17-1)(19-1) or simplified, 16*18 which is 288. Notice I said relatively prime, and not just prime. Obviously 288 is not a prime number (it’s even so we know that right off the bat). But we need to find a number it is smaller than 288, but is not able to divide it evenly. In this case, we’ll try the number 7 because 288 ÷ 7 = 5.9, meaning it is not a factor of 288. so e = 7.
- Now, it’s time to break out some algebra (don’t worry, it’s nothing to hard). We have to solve the equation e * d mod ((p-1)(q-1)) = 1. So lets fill in some variables that we already have answers to. 7 * d mod 288 = 1. So if you don’t remember, mod means the remainder after a division problem. So for example 21 mod 7 (21 ÷ 7) = 0 while 21 mod 8 = 5 (21 ÷ 8 = 2 with a remainder of 5). So what that d equals is literally open to countless possibilities, as long as the product of 7 * d mod 288 equals 1. For this case, we’re going to try d = 247. So lets try it out. 7 * 247 = 1729. 1729 mod 288 is 1 (1729 ÷ 288 = 6 with a remainder of 1).
So now we have all of the components we need to make a key. Our private key is a combination of e = 7 & d = 247. Our public key is a combination of n = 323 & e = 7.
I Have a Secret
So now it’s time to encrypt. For encryption, we use the recipients public key. We have a message we want to secure that says “I love Alice”. For simplicity we’re going to use the ASCII translation of these characters as noted below.
| I | l | o | v | e | A | l | i | c | e | ||
| 73 | 32 | 108 | 111 | 118 | 101 | 32 | 65 | 108 | 105 | 99 | 101 |
Now it’s time to process the first letter. The formula for Encryption (E) is E = M^e mod n. So lets expand that out. E = 73^7 mod 323 = 11047398519097 mod 323 = 112 = “p”. This translates to the following:
| 112 | 314 | 48 | 36 | 101 | 237 | 314 | 312 | 48 | 300 | 6 | 237 |
| p | 0 | $ | e | 0 |
Just a reminder that this is a very simple encryption scheme just to show how public keys works. Most encryption schemes make use of additional encryption to ensure that the same input in not represented by the same output further down the chain.
So why can’t we reverse this? In my unmathmatically trained mind, it comes down to that final mod in the formula. Remember with the mod, there is an infinite number of possible combinations that produce a mod 323. Combine that with the fact that while we know what e is (remember it’s part of the public key too), but there is a huge number of possible m values that when brought to the e power produce and mod 323 give us a value of 112.
I’ve Seen the Light
So now that we have received our encrypted message, it’s time to decrypt it. We do that with our private key. The formula to decryption this is M = E^d mod n. Again, using the first character which has an encrypted (E) value of 112…. M = 112^247 mod 323. 112^247 is a relatively large number. This translates to 1.434999003 E+506 mod 323. Or if we really want to write it all out:
143,499,900,366,499,581,498,871,604,658,645,132,576,327,728,533,543,657,866,496,696,064,083,713,934,301,248,623,292,748,003,401,219,676,103,929,947,816, 030,790,181,037,084,609,425,961,620,921,532,131,026,129,810,153,812,931,973,476,904,603,149,366,209,480,319,856,440,741,072,598,003,526,851,036,930,671, 064,728,412,818,980,795,689,216,812,623,392,261,848,726,072,834,807,375,497,581,710,176,409,105,438,143,863,380,185,018,422,482,225,619,431,558,131,856, 694,622,328,733,881,926,011,591,771,069,353,395,085,212,804,112,426,097,654,670,596,397,089,267,053,592,820,638,142,022,212,998,749,451,742,912,629,204, 085,207,115,713,546,493,007,551,319,470,131,764,573,232,754,065,408 mod 323
That = 73. When we put the entire message through, it comes back out to “I love Alice”
